What about for a six sided die?
Let’s take the coin-flipping example from last week and run a similar test on a six sided dice. Lets run a simulation from 1 to 5000 dice rolls and calculated the proportion of each number. For example, a 1 will be a single roll and we will count the number of each number (should be all zeros except for one value for one of the numbers). When we do 10 rolls, we will count the number of each number that pops up after each roll for 10 consecutive rolls.
set.seed(12345)
N_rolls<-data.frame(N = c(1:5000))
# Use sample to generate the roll simulations and lapply.
rolls<-lapply(N_rolls$N, sample, x=1:6, replace = TRUE)
# use table to count the frequencies of each roll
roll_counts<-lapply(rolls, table)
# Convert tables to data.frame (note we transpose the data)
rolls_count.df <- lapply(roll_counts, as.data.frame)
all <- do.call("rbind", rolls_count.df) # bind data together
# We need to specify which counts the rolls are associated with. we do this with rep and times
all$N_rolls <- rep(1:5000, times = sapply(rolls_count.df, nrow))
names(all)[1] <- "Roll_value" # Rename first columnUse tidyverse and dplyr to fill in missing Roll_value and turn to a percent
all %>%
complete(N_rolls,nesting(Roll_value), fill =list(Freq = 0)) %>% # Use complete to make sure we have counts for 1:6 for each roll
mutate(Roll_value = as.numeric(Roll_value)) %>% # Make sure the rolls are numeric
arrange(N_rolls, Roll_value) %>% # Change the order
spread(Roll_value, Freq) %>% # Long to wide format
group_by(N_rolls) %>%
mutate_each(funs(./N_rolls)) %>% # Change number of rolls to a percent
gather(Rollresult,value,`1`:`6`)-> Roll_prob # Change back to a long formatAnd plot this out.
ggplot(Roll_prob) +
geom_line(aes(x = N_rolls, y = value, colour = Rollresult)) +
geom_hline(aes(yintercept = 1/6), linetype ="dotted") +
facet_wrap(~Rollresult,ncol = 2) +
theme_bw() +
theme(legend.position = "none")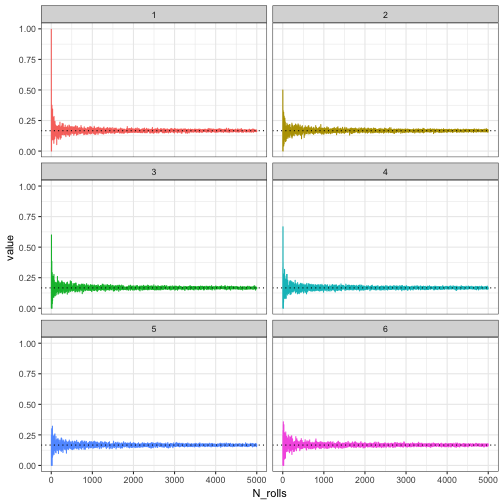
As expected, the more rolls we conduct the probability of any individual number approaches 0.167